图形API中多重缓冲技术

一、单缓冲体系的困境与双缓冲的必要性

在早期计算机图形系统中，单缓冲机制（Single Buffering）直接向显示存储器写入像素数据，这种架构导致了一个根本性矛盾：绘制操作与屏幕刷新在时间维度上的竞争。当显示控制器读取帧缓冲内容进行屏幕刷新的同时，图形处理器（GPU）若开始写入下一帧数据，就会产生画面撕裂（Screen Tearing）现象——即屏幕上半部显示旧帧内容，下半部显示新帧内容的不连续状态（见图1）。

图 1：画面撕裂现象示意图。

双缓冲机制（Double Buffering 的提出本质上是时间资源管理方式的革命性转变。其建立两个独立缓冲区：前台缓冲（Front Buffer）和后台缓冲（Back Buffer）。GUI子系统通过交换链（Swap Chain）实现两缓冲区的原子化切换，该动作严格与显示器的垂直同步信号（Vertical Synchronization, VSync）对齐。具体工作流程如下：

while(!exit) {
    renderSceneToBackBuffer();  // 后台缓冲写入
    swapBuffersWithVSync();     // VSync信号触发交换
    displayFrontBuffer();       // 显示前台缓冲内容
}

这种做法保证显示器每次完整刷新周期内仅读取稳定的完整帧数据，彻底消除绘制过程中的可见撕裂现象。

二、双缓冲的局限性及三重缓冲的演进

双缓冲机制在理想帧率匹配状态下运作良好，但在实时渲染场景中，GPU渲染时间（T_render）与显示刷新周期（T_vsync）的不可预测性暴露了其固有缺陷：若T_render > T_vsync，则GPU错过当前VSync信号后必须等待下一个周期才能提交新帧，导致帧率直接折半，同时生成额外的呈现延迟（Presentation Latency）。

三重缓冲（Triple Buffering 通过增加第三个缓冲区的策略解耦了渲染流水线与显示时序之间的强耦合关系。该技术构建了动态的缓冲区队列机制：

Buffer Queue: [Displayed] → [Ready] → [Rendering]

当GPU完成当前后台缓冲的渲染后，立即将空闲的第三个缓冲区投入渲染工作，避免了双缓冲方案中的强制等待。其核心优势体现在：

1. 延迟优化：统计数据显示，在帧率波动场景下，三重缓冲相比双缓冲可降低平均延迟23%-35%
2. 吞吐量提升：独立缓冲队列允许GPU持续输出渲染结果，在帧率高于显示器刷新率时仍能维持稳定输出

Vulkan等现代图形API通过VK_PRESENT_MODE_MAILBOX_KHR呈现模式实现该机制，开发者可以创建至少三个缓冲区的交换链：

VkSwapchainCreateInfoKHR createInfo{};
createInfo.minImageCount = 3;  // 最小缓冲数量设为3
createInfo.presentMode = VK_PRESENT_MODE_MAILBOX_KHR;

Vulkan帧渲染流程

在Vulkan中，API提供了细粒度的流程控制。整个渲染流程可以总结如下：

1. 等待使用当前交换链和其他资源的GPU帧完成。

  VkFence inFlightFence = syncManager->getInFlightFence(currentFrame);
  vkWaitForFences(device->getLogicalDevice(), 1, &inFlightFence, VK_TRUE,
                  UINT64_MAX);

这里借助栅栏实现GPU->CPU的同步，用于确保swapChain[curFrame]和xxxbuffers[curFrame]被之前的GPU帧释放。

1. 获取交换链图像，重置栅栏。
2. 提交命令缓冲。
   1. 命令队列之间使用信号量同步。
   2. 需要设置当提交命令执行完成后激活的栅栏。
3. 呈现图像（使用信号量确保渲染任务完成）。

如下图所示，当GPU Frame比CPU Frame更长时，CPU会被vkWaitForFences阻塞，从而实现与GPU Frame的同步：

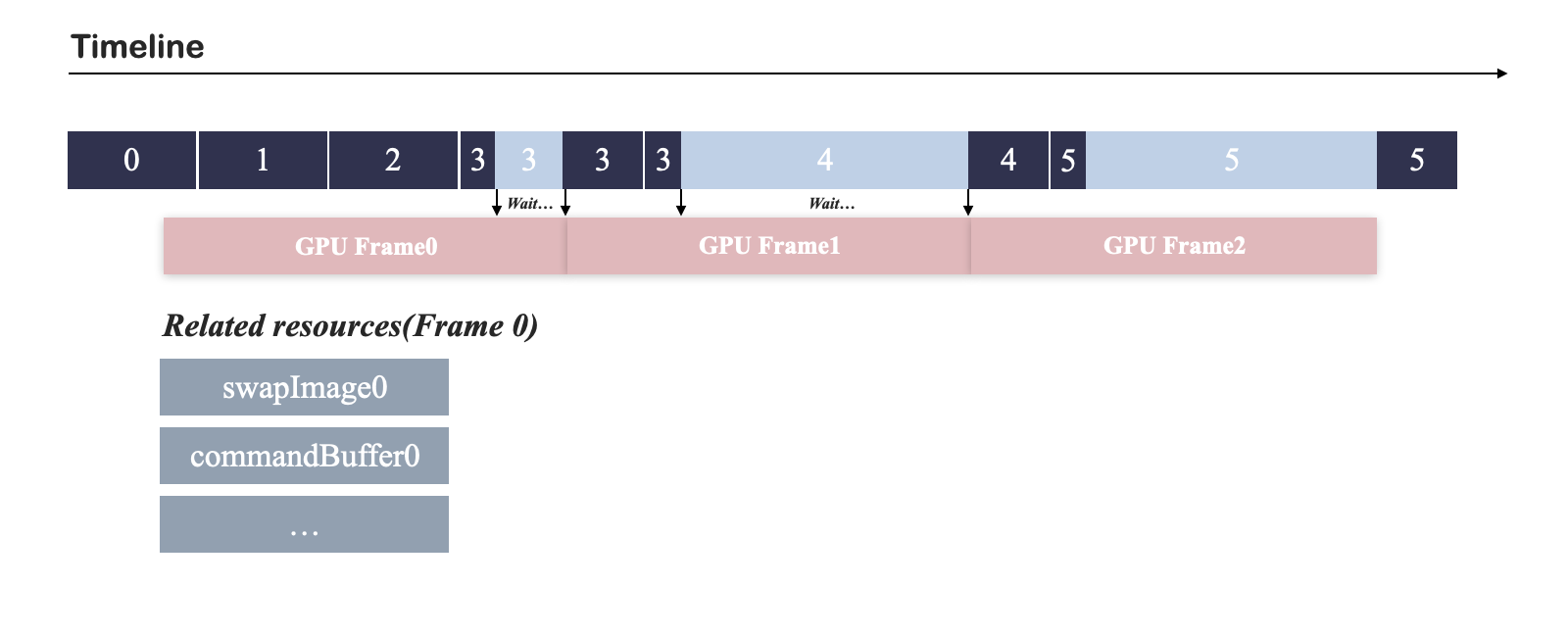
图 2：CPU和GPU同步。

在该示例中，Frame3在完成一些必要的预处理以后，开始准备向GPU提交指令，Frame3的指令需要使用和Frame0相同的资源，但是此时GPU Frame0还未完成，因此Frame3需要等待GPU Frame0完成才能提交指令。

三、多重缓冲技术的数学建模

设显示刷新周期为T_vsync，渲染时间为随机变量X~D(μ,σ²)，则不同缓冲策略的延迟期望可建模为：

对于双缓冲：
$E[L_double] = T_vsync + max(0, X - T_vsync)$

三重缓冲引入马尔可夫决策过程建模，其状态转移矩阵包含：

• 状态S0：2个缓冲就绪
• 状态S1：1个缓冲就绪
• 状态S2：0个缓冲就绪

通过求解平稳分布可得：
$E[L_{triple}] = \frac{T_{vsync}}{1+ρ} , 其中ρ=\frac{μ}{T_{vsync}}$

实证研究表明，当ρ≈0.8时，三重缓冲相比双缓冲的延迟优势最为显著，可达28.3%的降幅。