Calendar's Blog

homepage
Contents

Home > 技术学习 > GPU通用计算 > How to compute integral image on GPU?

How to compute integral image on GPU?
技术学习 2025-01-03 - -
user manual markdown writing format

Related Work

GPU Gems 3 (2005). Chapter: “Summed-Area Tables on the GPU” by Dave Johnson (NVIDIA).
https://developer.nvidia.com/gpugems/gpugems3/part-ii-light-and-shadows/chapter-8-summed-area-variance-shadow-maps

Parallel Prefix Sums
https://developer.nvidia.com/gpugems/gpugems3/part-vi-gpu-computing/chapter-39-parallel-prefix-sum-scan-cuda
Scan primitives for GPU computing

GPU-efficient recursive filtering and summed-area tables
https://dl.acm.org/doi/10.1145/2070781.2024210

技术重点：
并行前缀和（Scan）：大多数GPU实现将积分图像计算分解为两个主要的并行前缀和传递，一个是水平方向的，另一个是垂直方向的。
内存合并与冲突：高效的GPU积分图像算法注意内存布局，确保线程访问连续的内存段以减少延迟并提高吞吐量。
工作负载划分（Tile）：大型图像被划分为独立且并行计算的小块。在每个小块上计算出部分总和后，额外进行一次合并操作以得到全局积分图像。
层次化方法：层次化求和策略通过将求和问题拆解成多个阶段来降低处理大型图像时所需处理复杂度。
使用共享内存与寄存器：高性能实现将中间总和保存在在快速GPU共享内存中，从而减少全局内存流量。

Summed-Area Variance Shadow Maps(GPU gem3)

https://developer.nvidia.com/gpugems/gpugems3/part-ii-light-and-shadows/chapter-8-summed-area-variance-shadow-maps
该章节指出SAT的计算本质上是两个维度的前缀和过程。Hensley et al. 2005.提出了一种更并行的方法。
本章节主要关注积分图像计算时的精度问题，Hensley et al. 2005有很多关于精度问题的解决方案， Donnelly and Lauritzen 2006也给出了一种解决方案。

Parallel Prefix Sum (Scan) with CUDA（GPU Gem3）

Naive Method

CPU的前缀和计算的复杂度为O(n),GPU算法的复杂度如果不超过该复杂度，我们称之为efficient work。
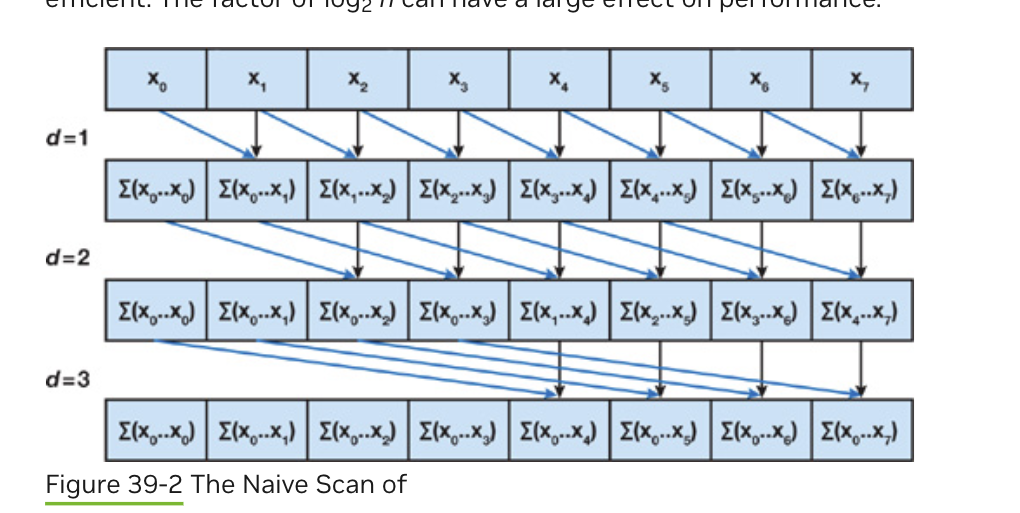
image.png
最原始的GPU版本就是一个不高效的实现，该算法需要两个Buffer来保证正确性。同时，该算法还假设处理器单元的数量和数组大小一致。

Work-Efficient Method

  • 使用平衡树来优化复杂度。
  • 分成两个过程，Red1uce(归约过程，也被称作上扫过程)；和下扫过程。
  • 同一个位置上的操作在共享内存中完成。

Reduce
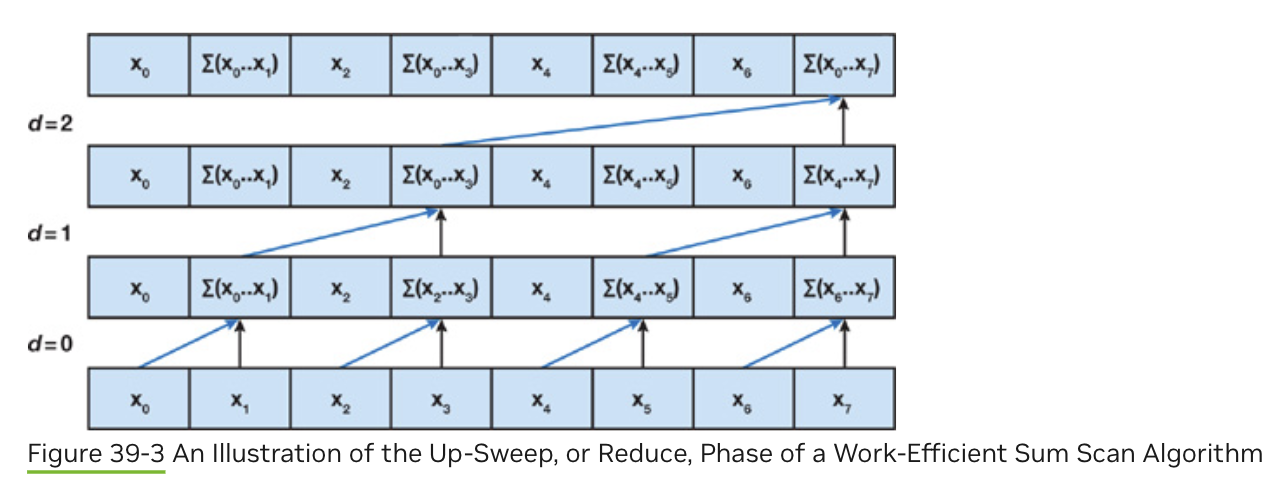
image.png

image.png
该过程结束后，根结点上保存了整个数组的和。

down-sweep
image.png
在上扫描阶段，我们已经获得了总和，但前缀和还未完全计算出来。下扫描阶段通过逆向操作，逐步填充前缀和数组。
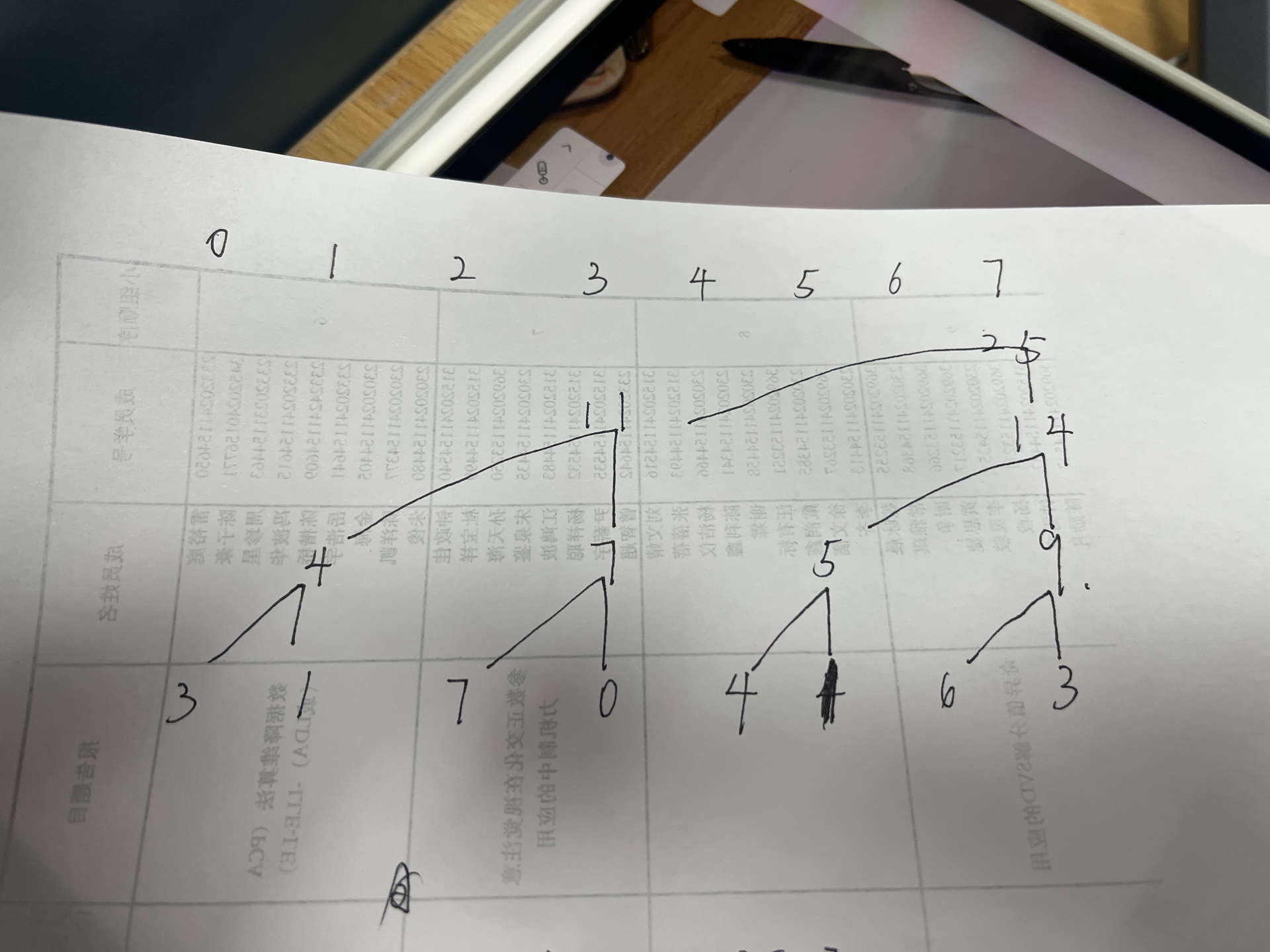
图像.jpeg
上扫描结束后，位置0，1，3，7的值是前缀和数组中会出现的值（为inclusive的，但通常需要计算exclusive的）。例如，25的右子树14需要11的值来更新子节点。
因此，下扫描过程可以理解为一个传递到左子树、累加右子树的过程。

  1. 初始化：设置根节点为0.
  2. 遍历步长数组[4,2,1]
    1. 设置左子树为根节点的值，右子树为左子树和右子树的和（左子树使用设置后的值）。

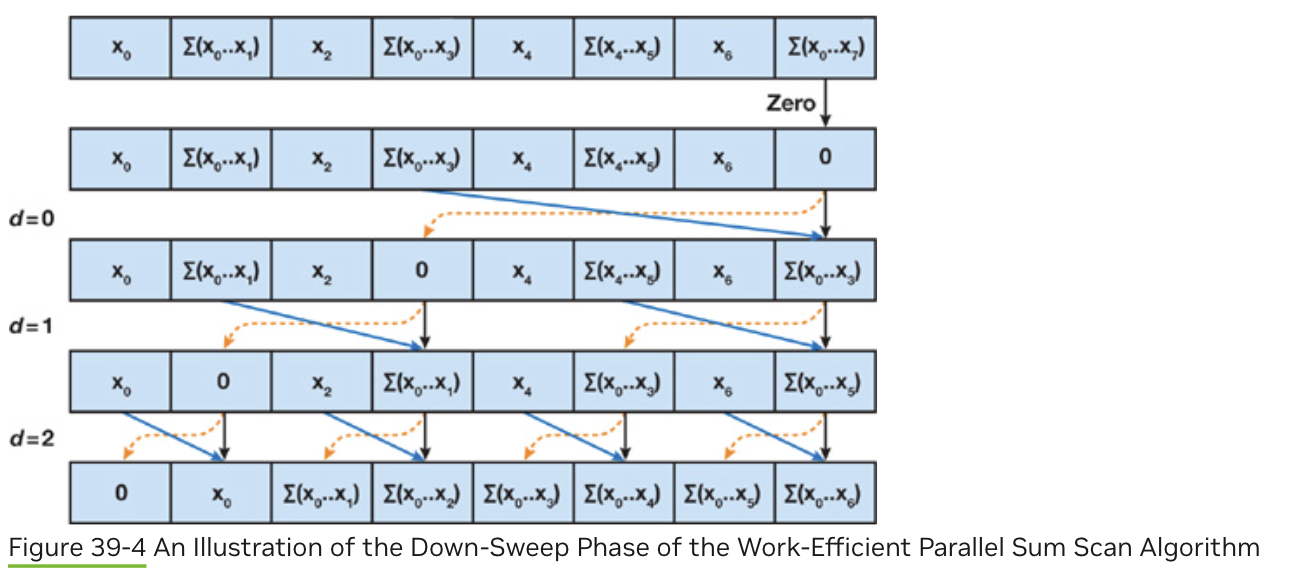
      该过程一个线程操作两个元素，需要在同一个work group中完成。
      使用上扫阶段的结果：
      • 树结构： 
           25
 /    \
   11      14
  /  \    /  \
 4    7  5    9
/ \  / \ / \  / \
  3  1 7  0 4 1 6 3
  • 初始化根节点为 0： 
            0
      /    \
    11      14
   /  \    /  \
  4    7  5    9
 / \  / \ / \  / \
3  1 7  0 4 1 6 3
  • 传递并更新：
    • 根节点 0 分配给左子树 left = 0 和右子树 right = 11（左子树的部分和）。
    • 左子树 11 分配给其左子树 left = 0 和右子树 right = 4。
    • 右子树 14 分配给其左子树 left = 11 和右子树 right = 5。
    • 继续递归，最终得到前缀和数组。

最终前缀和数组 S = [0, 3, 4, 11, 11, 15, 16, 22]。

Fast Summed‐Area Table Generation and its Applications[Hensley et al. 2005]

提到论文：Simple Blurry Reflections with Environment Maps 似乎是使用miomap近似模糊的lerp blur。

方法

使用图形管线实现，整个过程分解为两个phase，每个phase包括log(n)个pass。
使用两张纹理图像，互相作为输入输出。
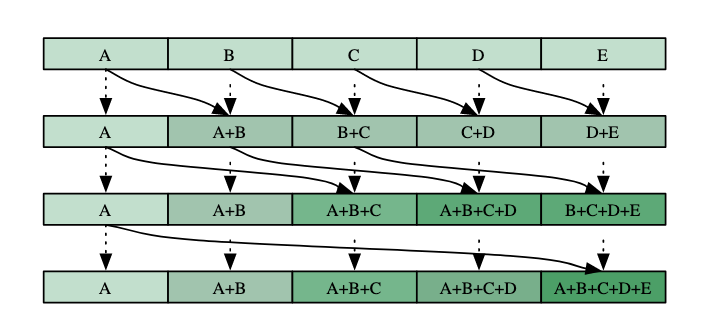
image.png

积分图像的精度问题

  1. 累加时机器误差的积累。
  2. 使用积分图像时通常是两个接近的值相减，尤其是两个值很大时，误差会更加明显。
  3. 积分图像的最大值大小为$w \times h \times 255$

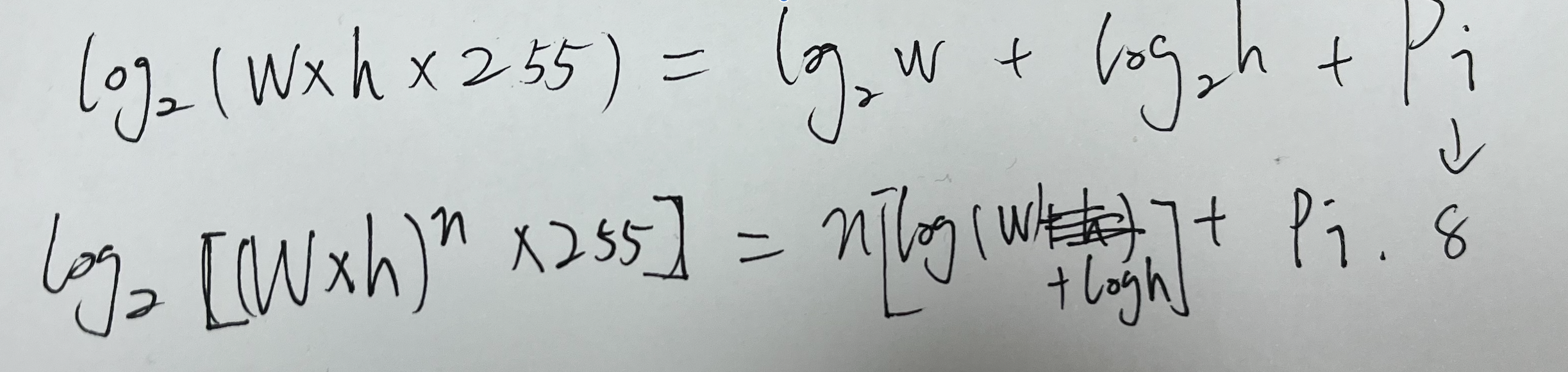
image.png

Using Signed-Offset Pixel Representation

将像素值进行偏移，从[0,1]偏移到[-0.5,0.5],这样可以使得：

  1. 数值不总是单调的。
    有两种方式实现这一点：
  2. 所有像素值-0.5.
  3. 所有像素值-平均值。

Using Origin-Centered Image Representation

以图片的中心点作为原点，相当于计算四张更小的积分图像，从而避免了极大值的出现。
但是使用时增加了额外的计算量。

Scan Primitives for GPU Computing 2007

GPU并行模型

符合流水线结构的算法天然适合GPU实现。即，每个kernel处理单独的输入，产生单独的输出。
某些问题，例如前缀求和问题，需要输入数据的全局知识。

相关工作

原始方法

horn 2005
[[#Fast Summed‐Area Table Generation and its Applications[Hensley et al. 2005]]]
这些方法的复杂度为O(nlogn)，是non-work-efficient的。

reduce and down-sweep

提出：Blelloch in 1990[Vector Models for Data-Parallel Computing]
GPU实现：Sengupta(本文作者) et al. and Greß et al. in 2006
CUDA实现：本文

方法

本文方法的主要贡献是引入了分段扫描的概念.
分段扫描Segmented Scan，是一种将输入序列分成多个互不影响的字序列并进行后续操作的过程。
使用flag数组标记不同的分段，例如：
Data: [a, b, c, d, e]
Flags: [1, 0, 1, 0, 0]

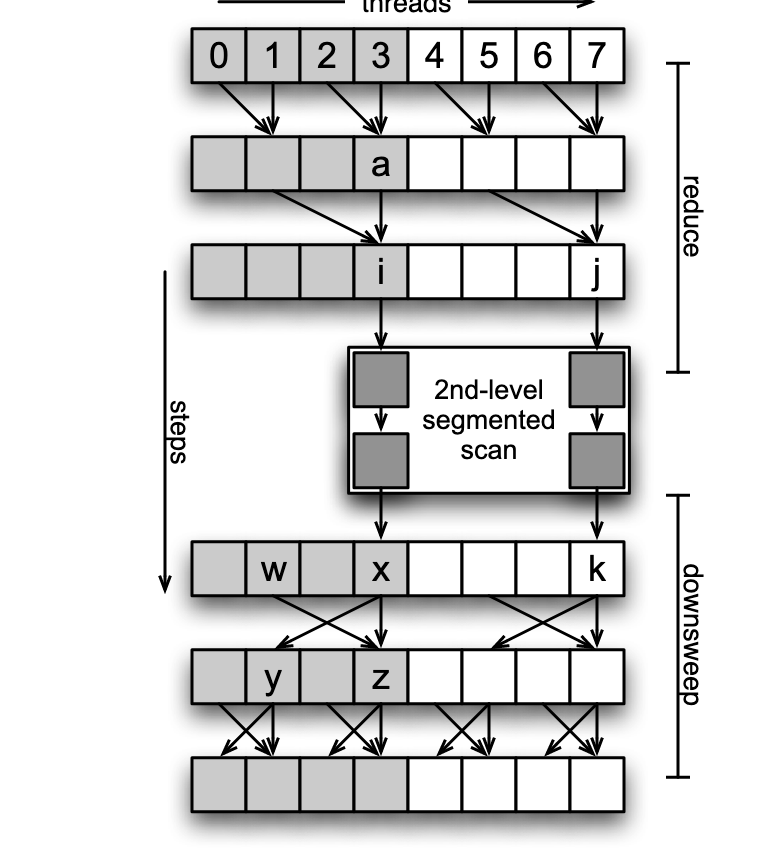
image.png
该算法用于解决输入向量超过线程块大小的情况。
在归约过程和下扫描之间插入部分和的计算。
（影响下扫描的初始化）

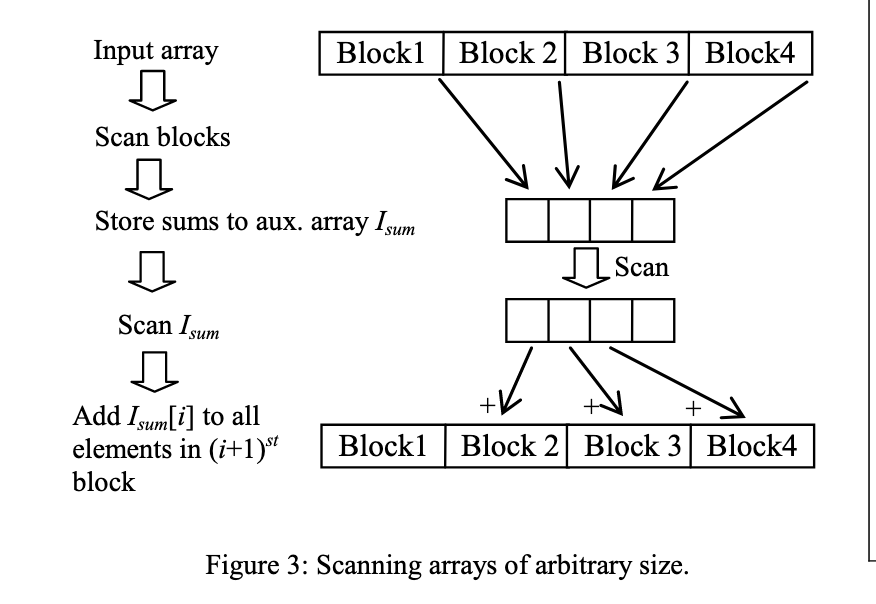
image.png

Efficient Integral Image Computation on the GPU 2010

使用work-efficient的前缀和计算，利用了分段扫描解决大数组问题。积分图像的计算转化为：前缀和-转置-前缀和过程。
使用tanspose操作的优点在于，可以使用同一个kernel完成两次扫描操作。
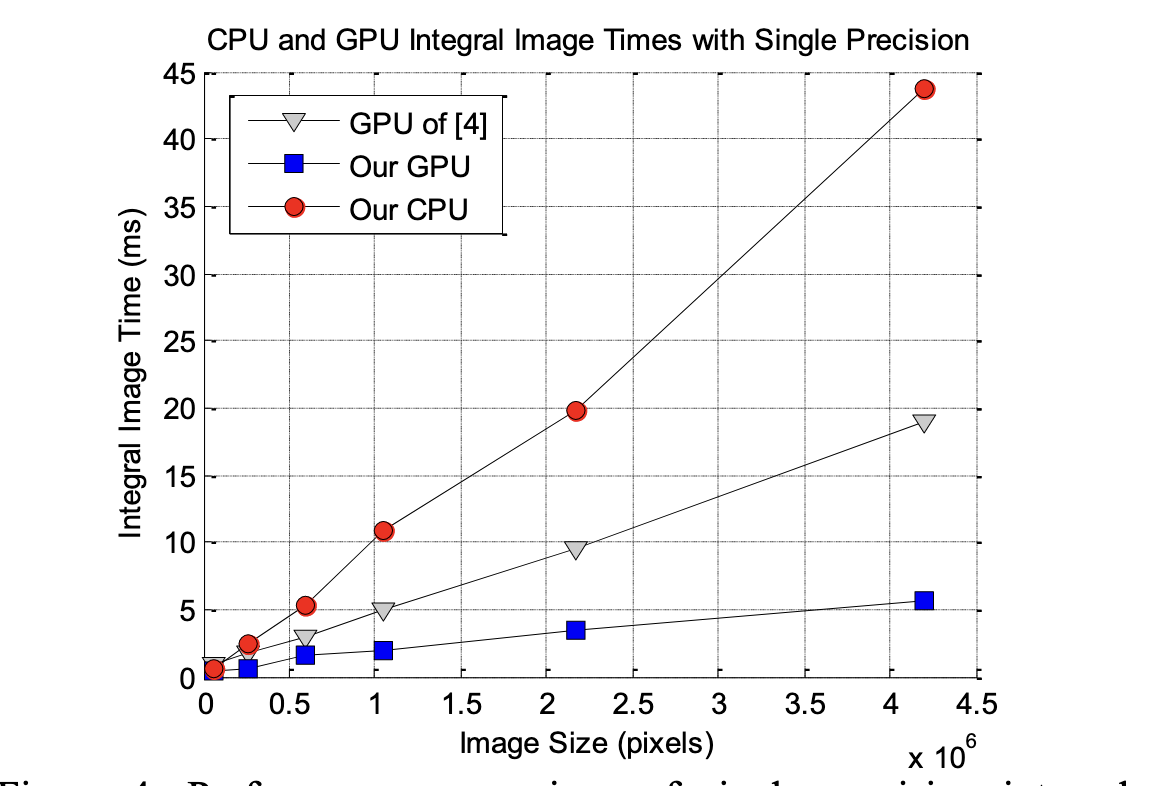
image.png

GPU-Efficient Recursive Filtering and Summed-Area Tables 2011

Efficient Algorithms for the Summed Area Tables Primitive on GPUs 2018

Scan-scan algorithms:

  • Compute prefix sums directly
  • Limited by memory access patterns

Scan-transpose-scan algorithms:

  • Use matrix transposition between steps
  • Rely heavily on scratchpad memory
  • Have expensive matrix transpose operations
  • Face memory bandwidth limitations
    该方法来自于Efficient Integral Image Computation on the GPU。本文指出，该方法需要对global memory的聚合访问和昂贵的transpose操作。

    [!聚合访问]
    对全局内容的访问较慢，只有每一个线程以相同stride的方式访问全局内存，才能实现峰值吞吐：
    Thread 0: accesses address N 
    Thread 1: accesses address N+1 
    Thread 2: accesses address N+2 
    …and so on

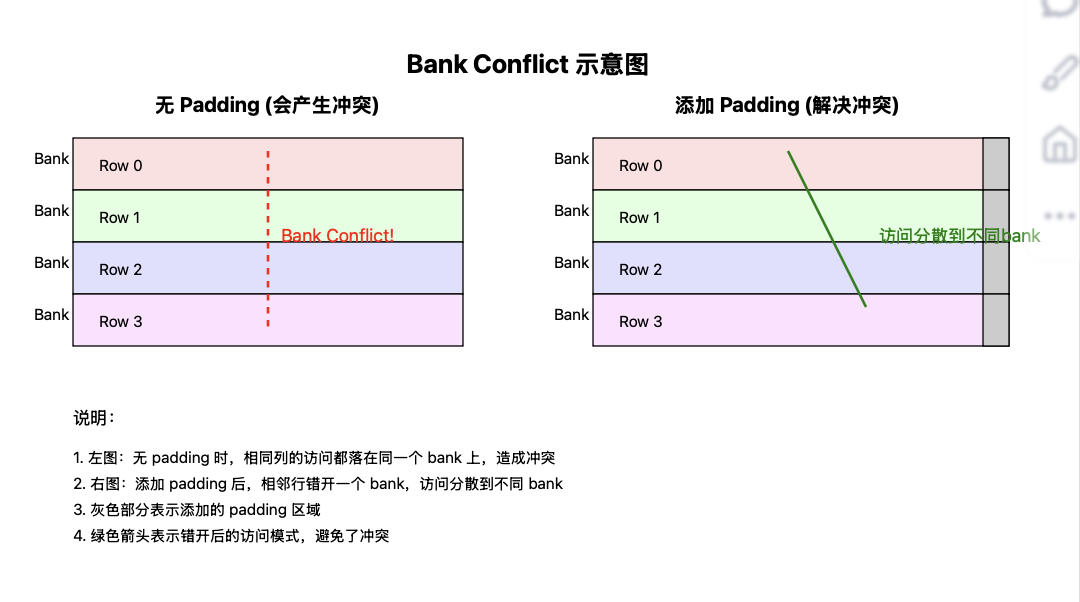
[!bank conflict]
现代GPU的共享内容被分成一系列的bank。当同一个warp中的不同线程访问同一个bank时，会发生冲突。
例如，一个warp中存在12个线程，每个线程都需要访问共享内存对应行的32个数据，即第i个线程访问sharedMem[i][0…31]由于bank的存在，每个线程访问数据j时都对应到同一个bank中，因此存在冲突。
本文为了避免这种冲突，定义数组大小为[32][33]
image.png

本文方法的动机

SAT 计算的瓶颈在于数据移动。以聚合模式高效访问全局内存对算法性能至关重要。此外，设计减少为了减少数据移动，我们采用了寄存器缓存方法。问题在于如何在有效使用寄存器的同时避免争用。
线程间通信寄存器的技术（即shuffle指令）只能在单个 warp（CUDA 中一起执行的一组线程）内工作。因此，我们调整了算法，在warp级别进行扫描，同时避免warp内部通信。

最直接的SAT计算

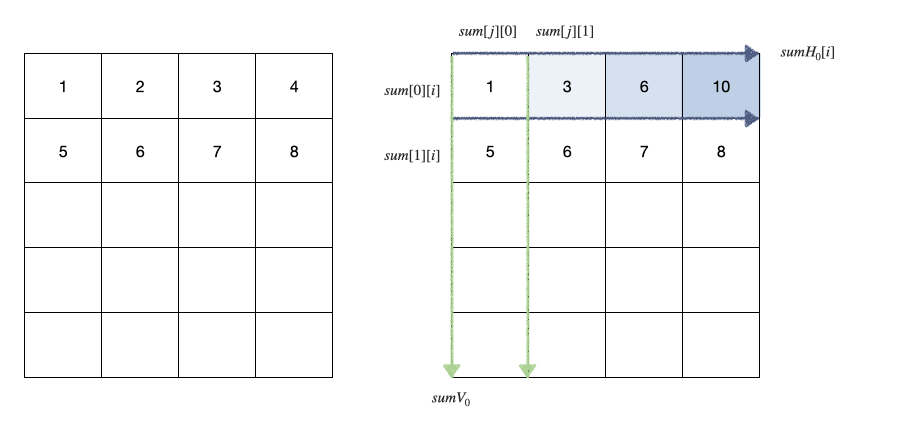
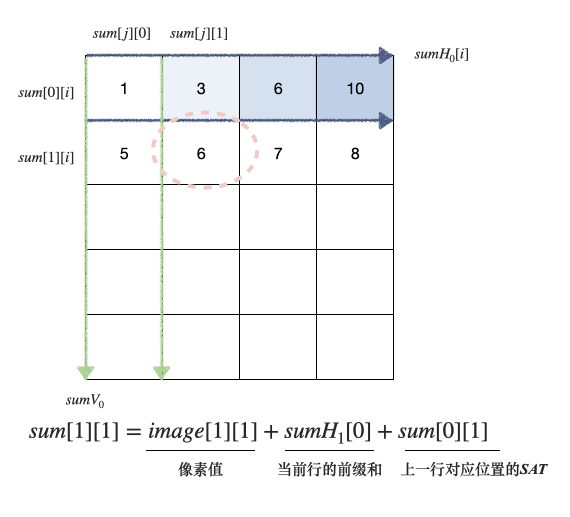
image.png
image.png
image.png

Prefix Sum

Basic method

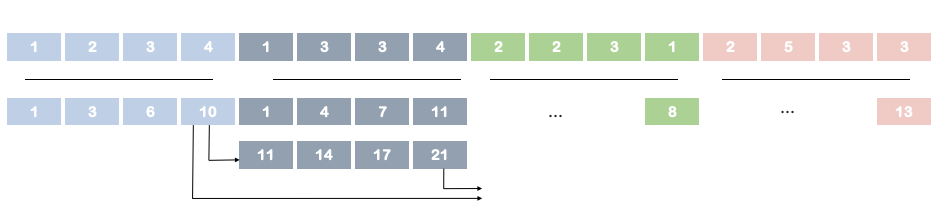
image.png

Kogge-Stone

http://lumetta.web.engr.illinois.edu/408-S20/slide-copies/ece408-lecture16-S20.pdf
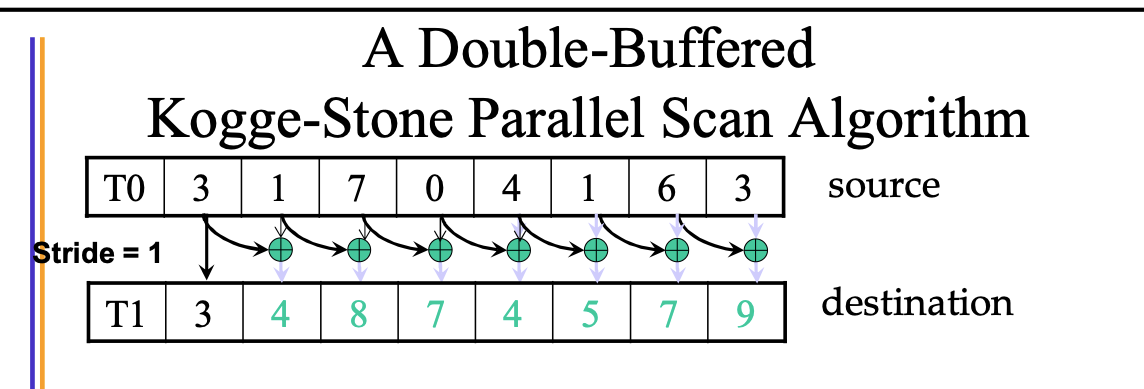
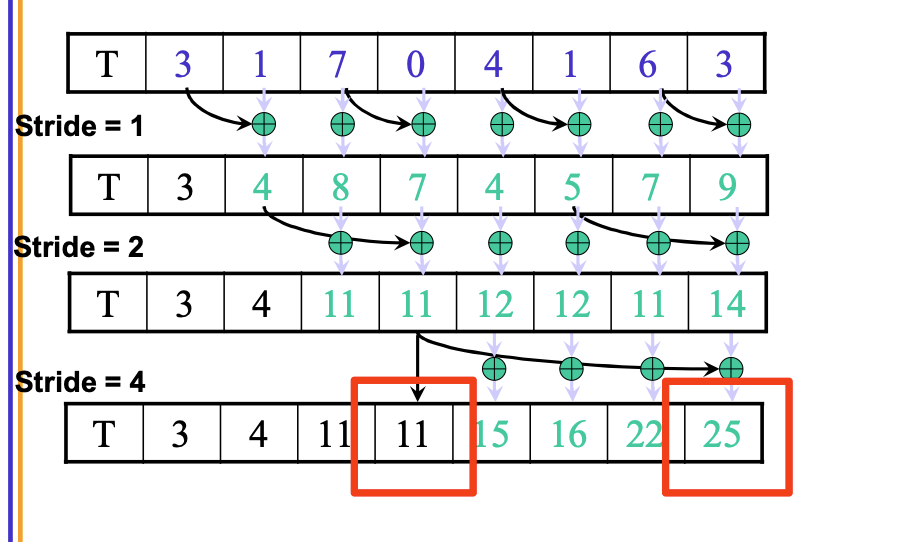
image.png
image.png
Step1得到长度小于等于2的累加和
Step2得到长度小于等于4的累加和
Step3得到长度小于等于8的累加和

LF-scan

warp shuffle
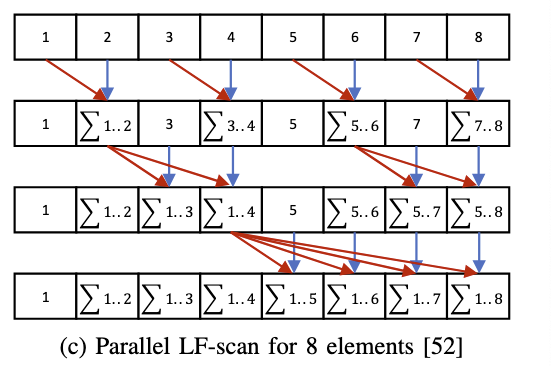
image.png

In theory, the LFscan achieves the highest computing efficiency with logN stages and $\frac{NlogN}{2}$
addition operations as Fig. 2c shows,

‘reduce (up-sweep) and down-sweep’

https://developer.nvidia.com/gpugems/gpugems3/part-vi-gpu-computing/chapter-39-parallel-prefix-sum-scan-cuda
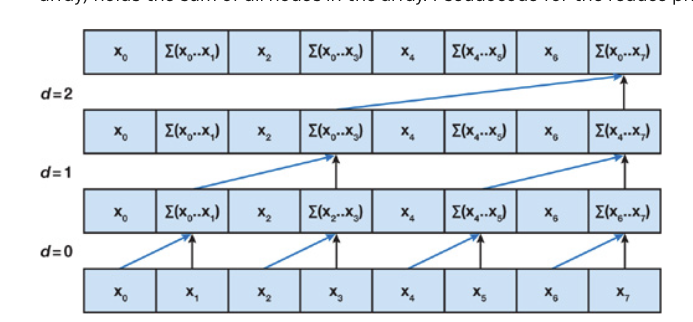
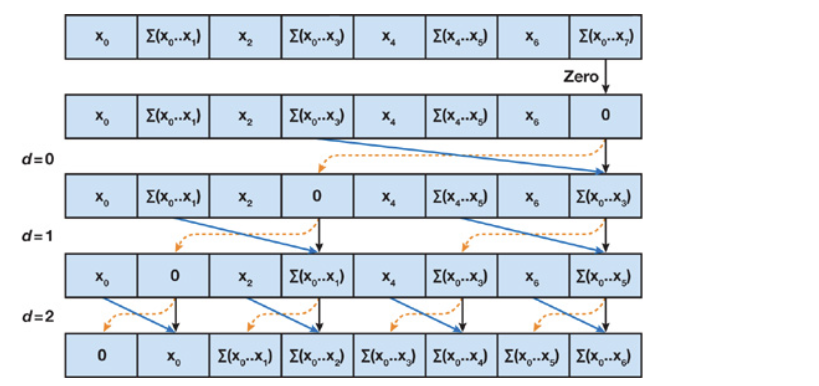
image.png
image.png

问题

  1. 算法流程决定加法运算的次数和算法阶段数。
  2. 数据存储、传递的方式(GPU显存访问模式)也会显著影响算法性能。

本文贡献

  1. 使用寄存器存储中间数据。
  2. 提出BRLT

方法

Caching Data Using Register Files

SAT的计算问题是内存限制的。
每个线程都先使用寄存器缓存数据。
并且warp中线程的通信泗洪shuffle操作完成。

GPU聚合访问

用于降低对Global Memory的访问成本。具体做法是，在同一个warp中的所有线程访问临近的内存位置。GPU可以将这些操作打包成一次数据传输，从而降低延迟、提升带宽。

  1. data向16 bits or 32 bits对齐。
  2. globalID = (x + width * y + width * height * z),对内存位置的访问和GlobalID一致（尤其是2D图像，y连续访问不是聚合访问）。

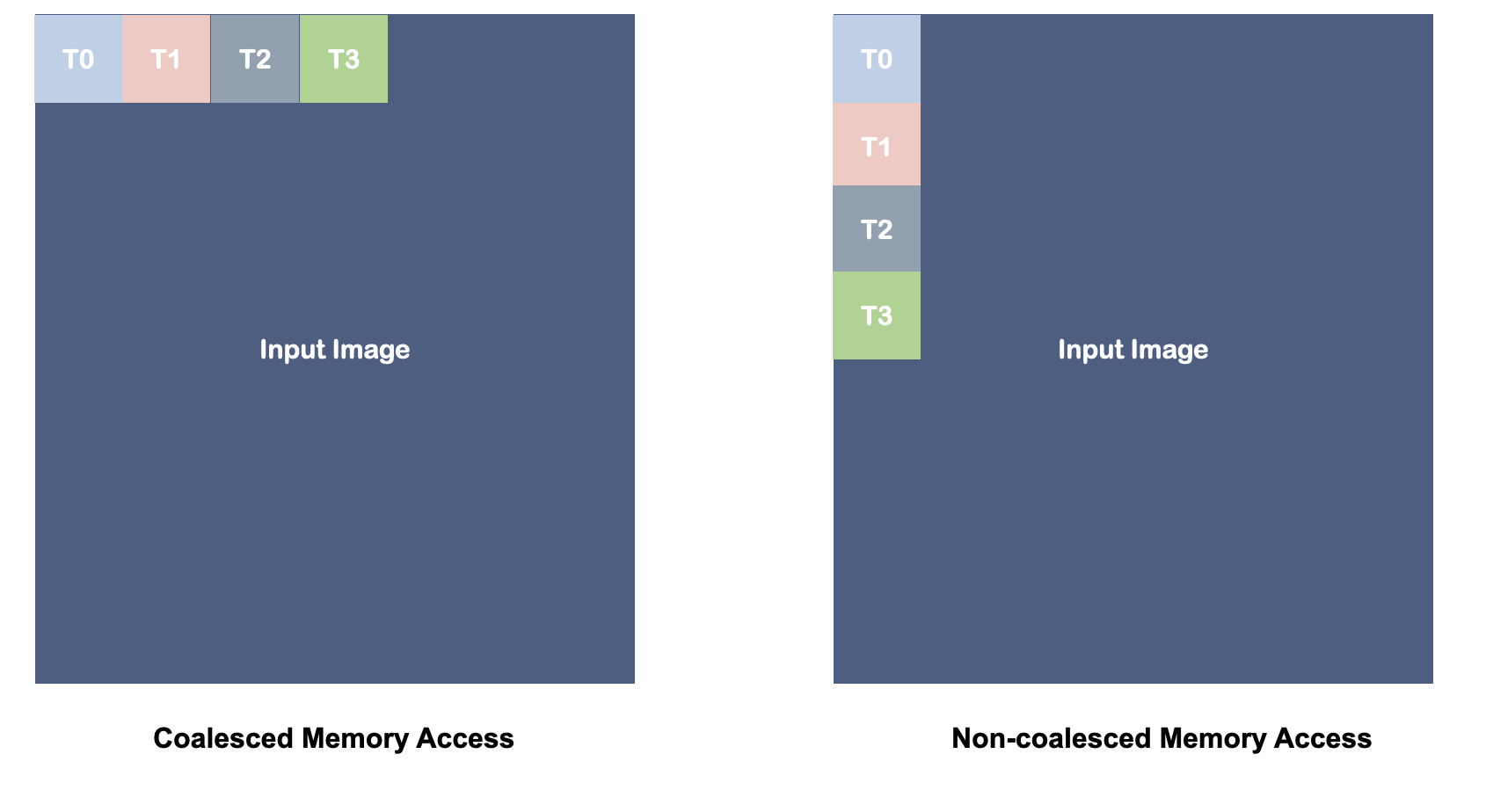
image.png

Google
Ch

问题回顾

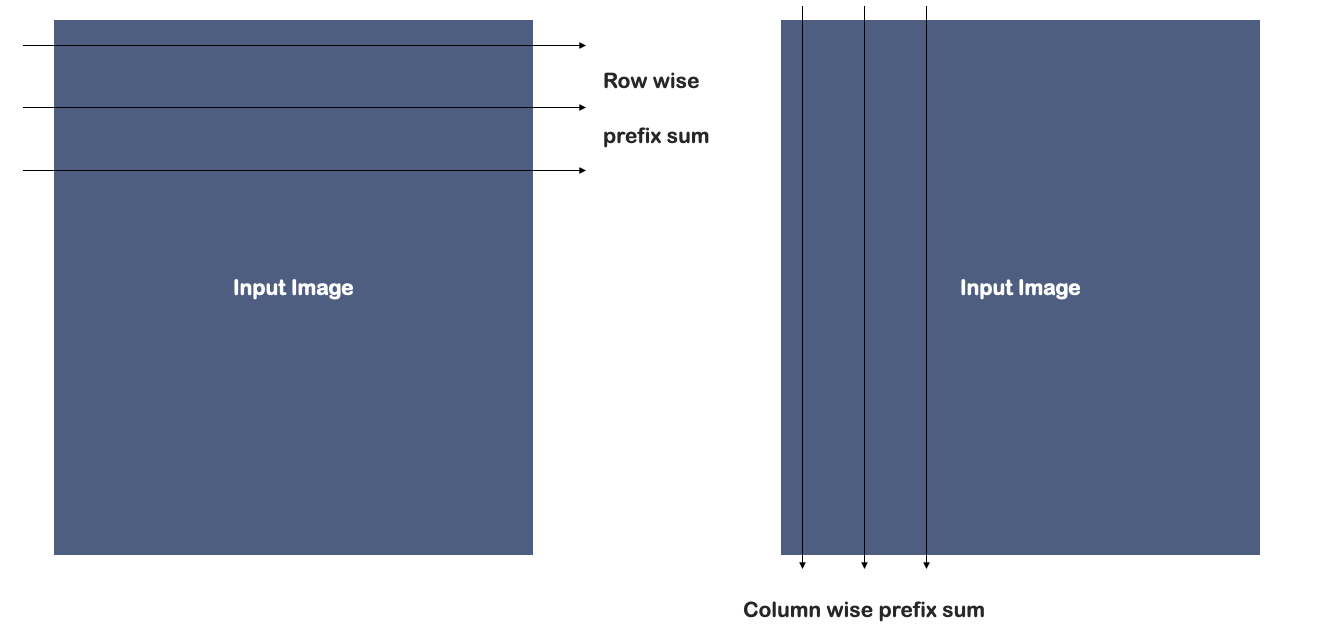
image.png
计算前缀和在两个方向上进行。
但是：

  1. 两个方向需要使用不同的kernel函数（不同的着色器程序，或者引入不同的分支）。
  2. 列方向处理的数据不连续，无法实现聚合访问。

因此，SAT计算更常见的做法是Scan-transpose-scan。
接下来需要考虑矩阵转置是否是聚合操作。

矩阵转置

warp level

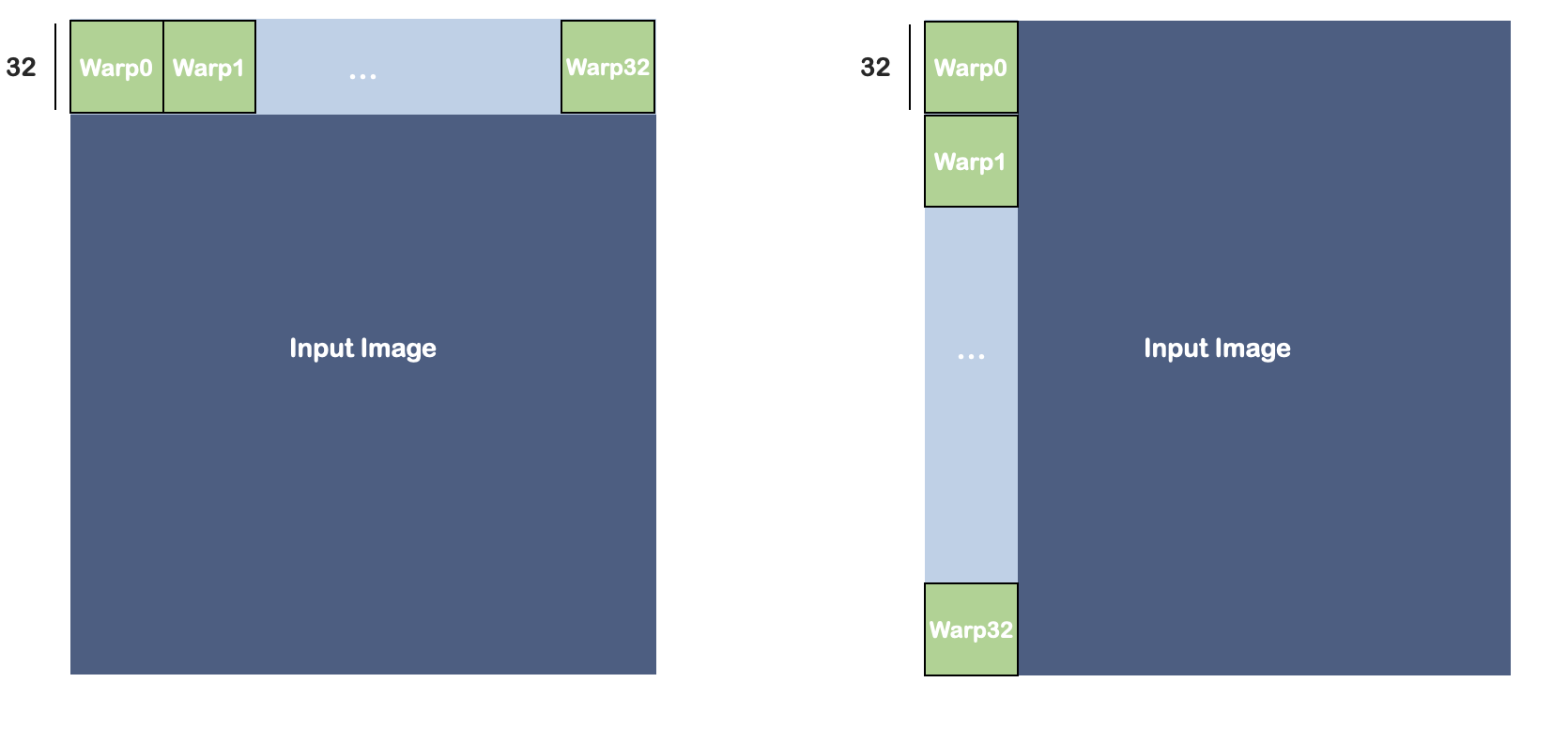
image.png

element level

在每个warp内部：
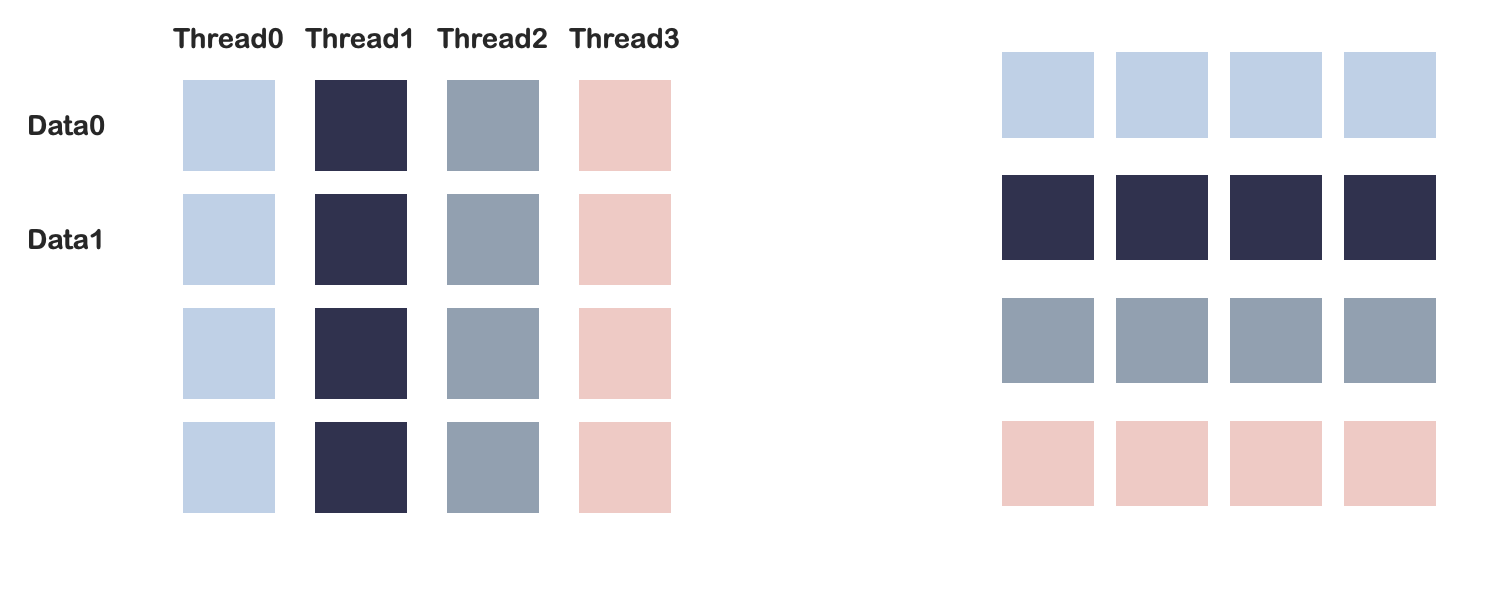
image.png

Method：直接做法

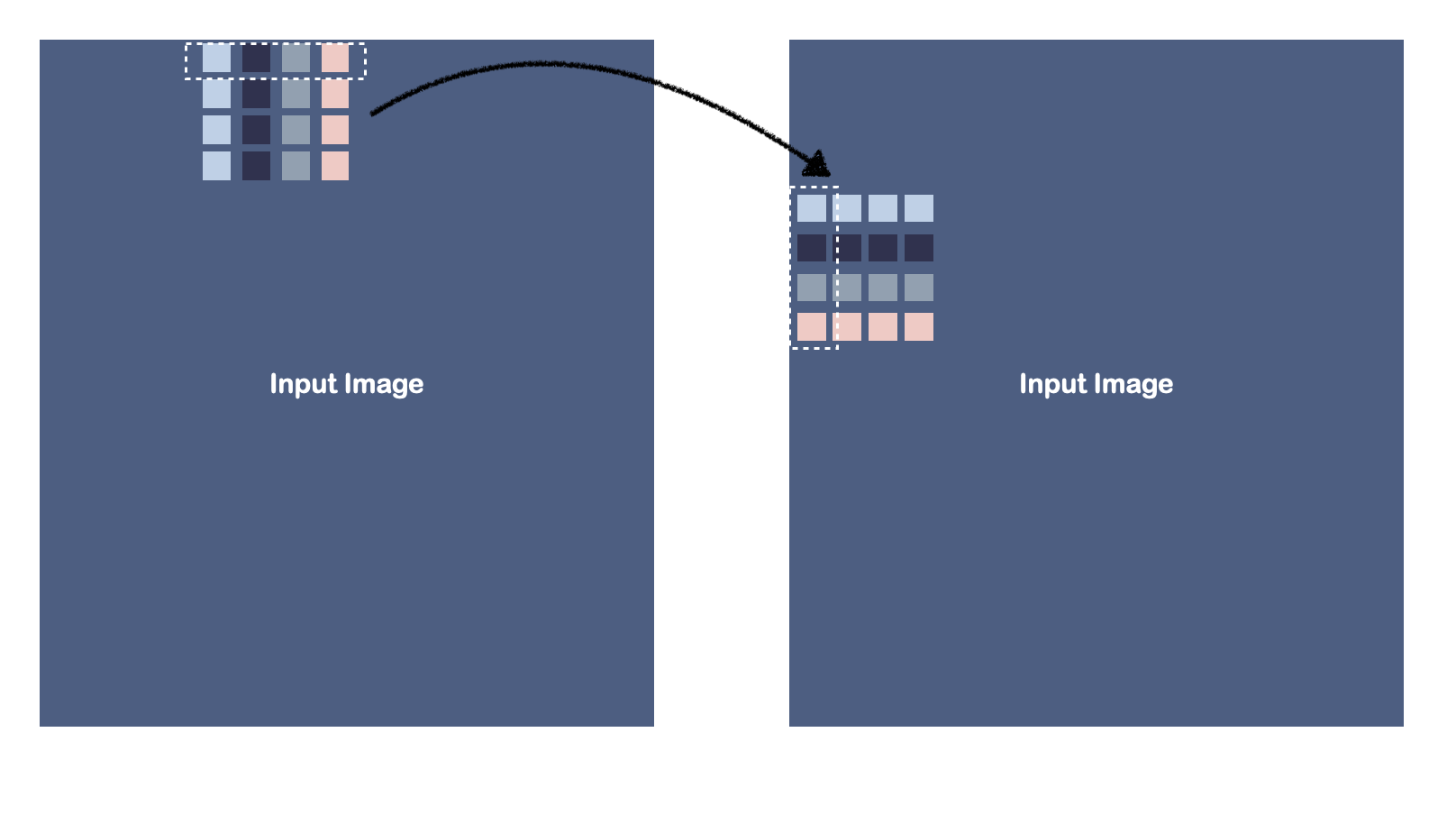
image.png
写入操作不是聚合操作。
本文提出了BRLT，在Shared memory中对warp中的数据进行转置。

BRLT

Block-Register-Local-Transpose Method
这是一种将数据从寄存器复制到共享内容再复制回寄存器的矩阵transpose方法。
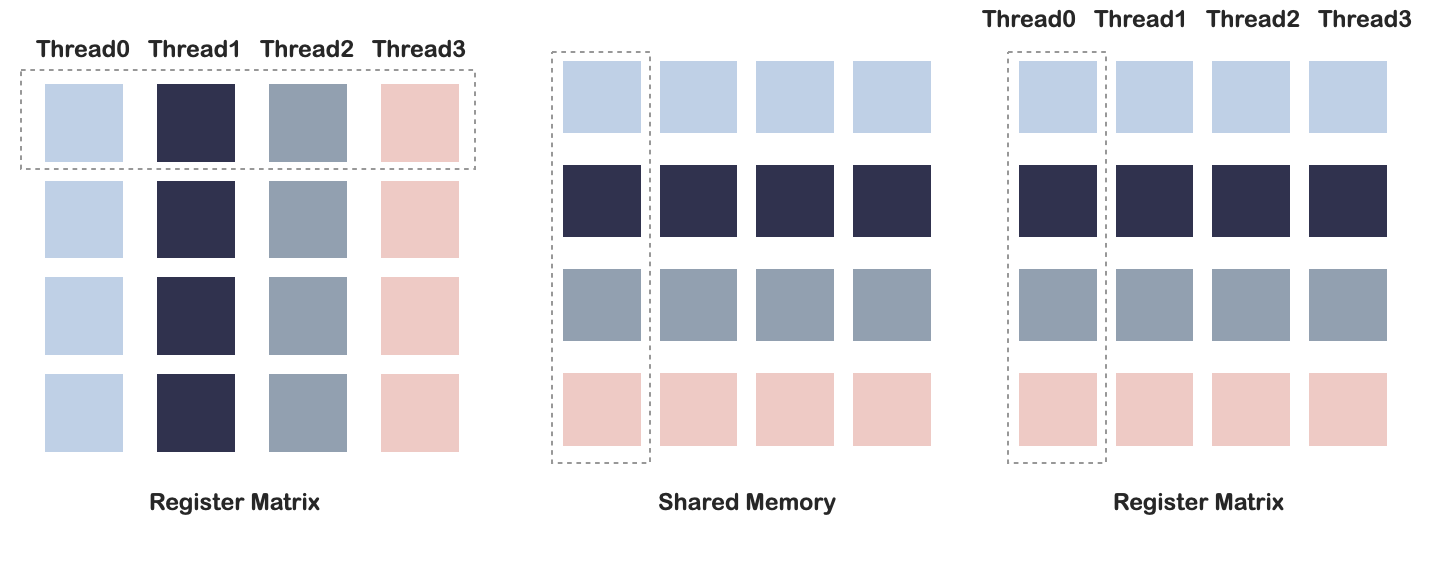
image.png

这种方法的仅使用共享内存作为缓冲区，transpose操作是在寄存器-共享内存之间完成的；传统算法的操作是在共享内存中完成，并且需要从主存中加载数据。

Bank conflict

google
GPU共享内存以bank的形式被组织。N卡通常32banks，bank中数据单元大小为4或8。当一个warp中的不同线程访问到同一个bank时，会发生conflict，导致IO操作无法并行。
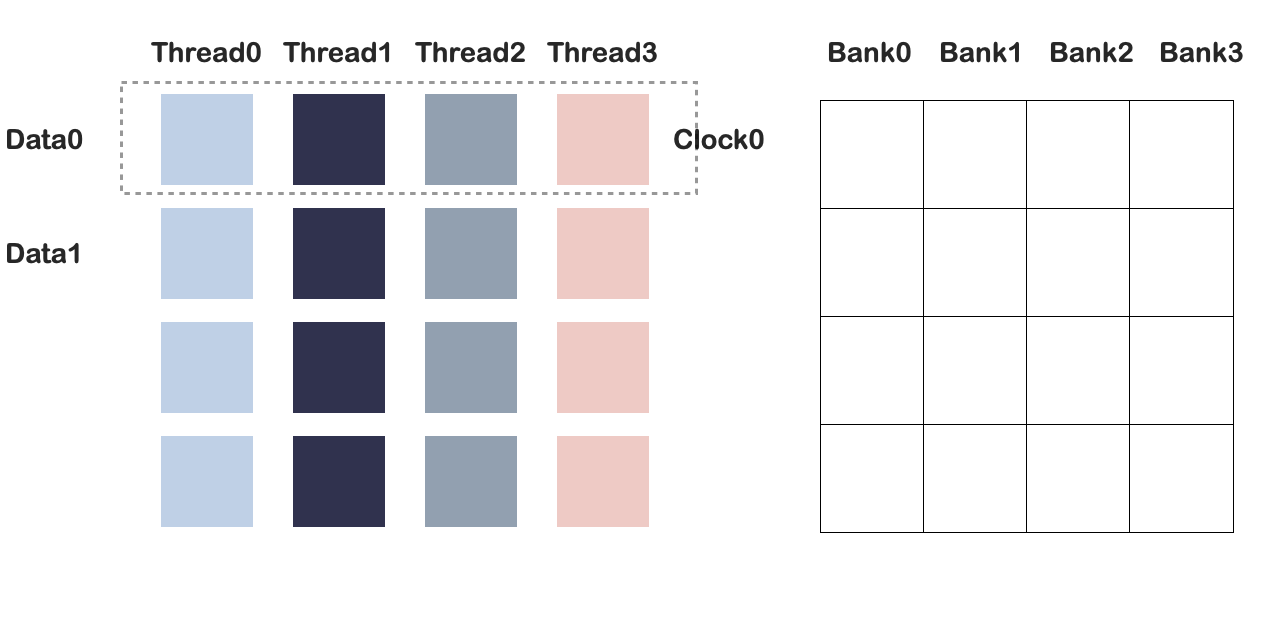
image.png
例如，bank number=4.该任务是一个矩阵转置任务，Clock0时，四个线程写入第一列：
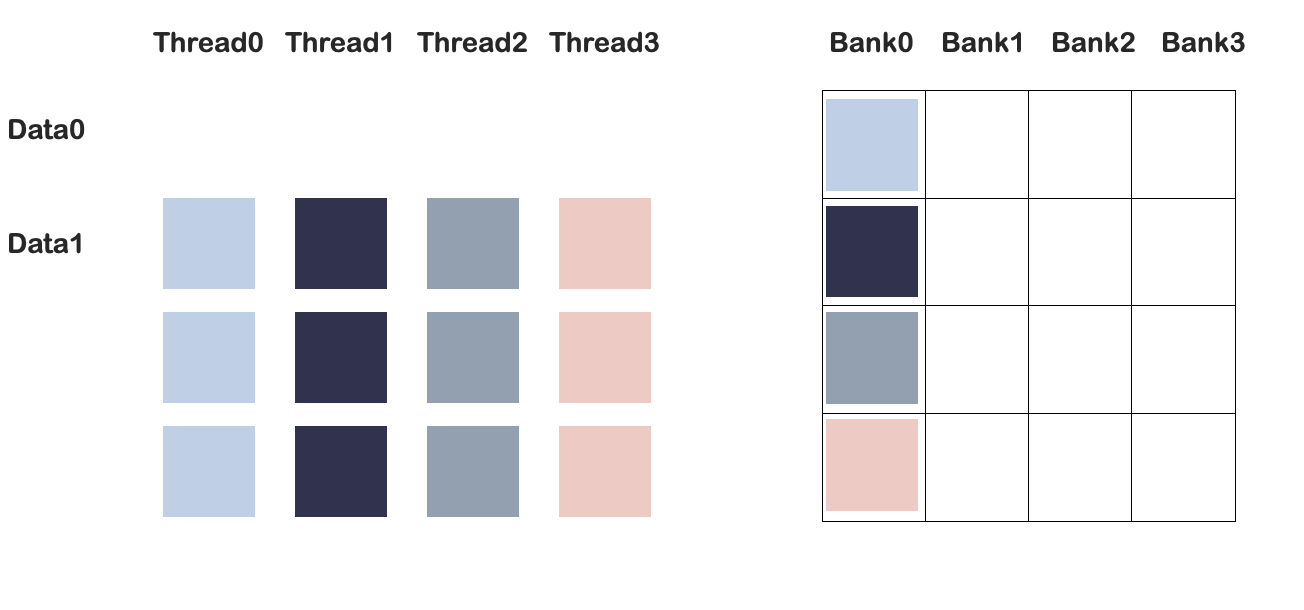
image.png
此时发生bank conflict。
但是如果修改共享内存大小为4*5:
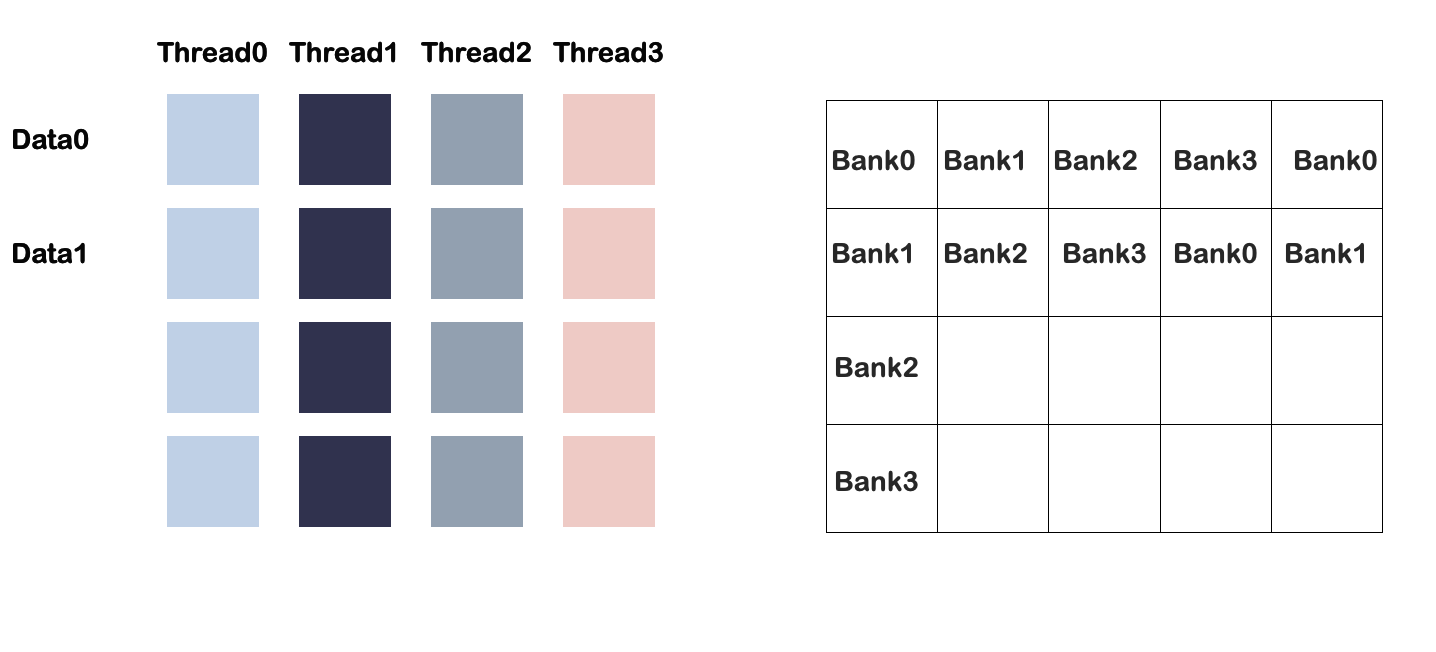
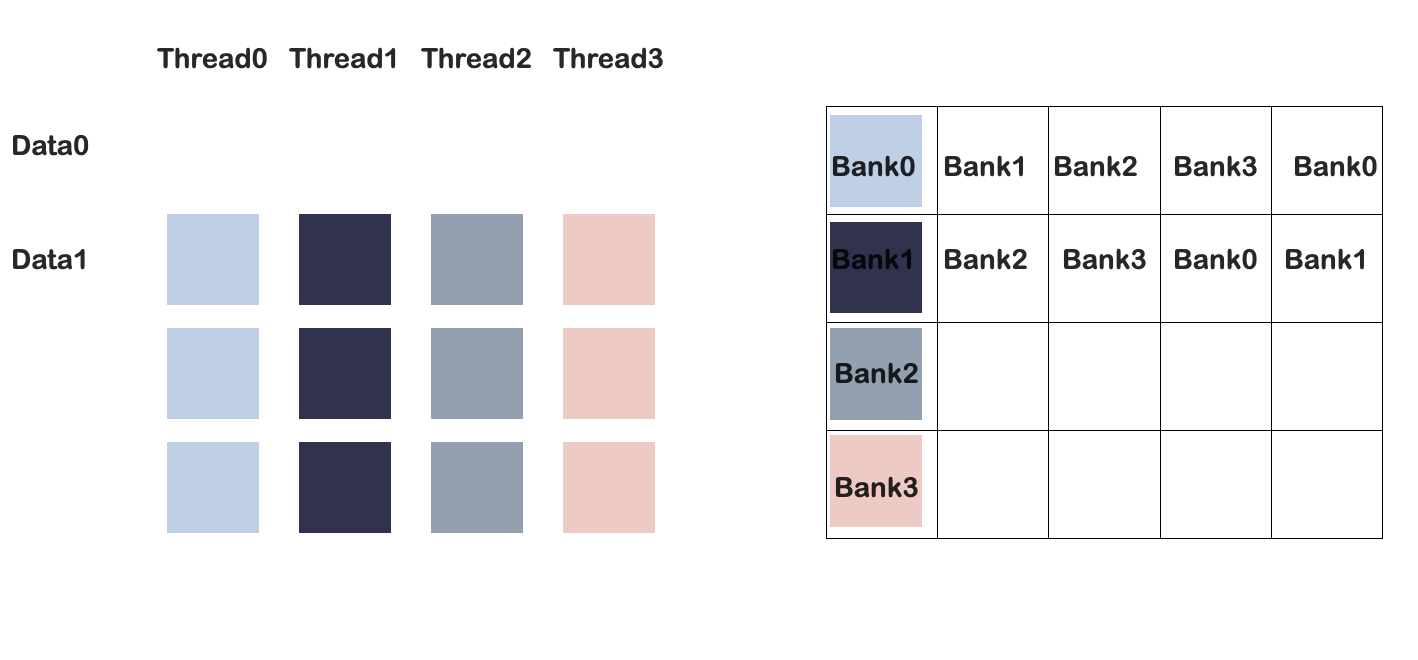
image.png
image.png

部分和计算

  1. 将warp计算出的部分和存储在共享内存中。
  2. 在共享内存中计算数据的前缀和。
  3. 将数据从共享内存加载回对应的warp。

方法一：ScanRow-BRLT

Efficient Integral Image Computation on the GPU 2010中方法需要将行扫描的结果存储在全局内存中，transpose操作也在全局内存中完成。
本文中的方法:

  1. 将输入2D图像的一块直接加载到block中,
  2. 然后执行行扫描-BRLT-写回主存。因此转置操作在共享内存中完成。
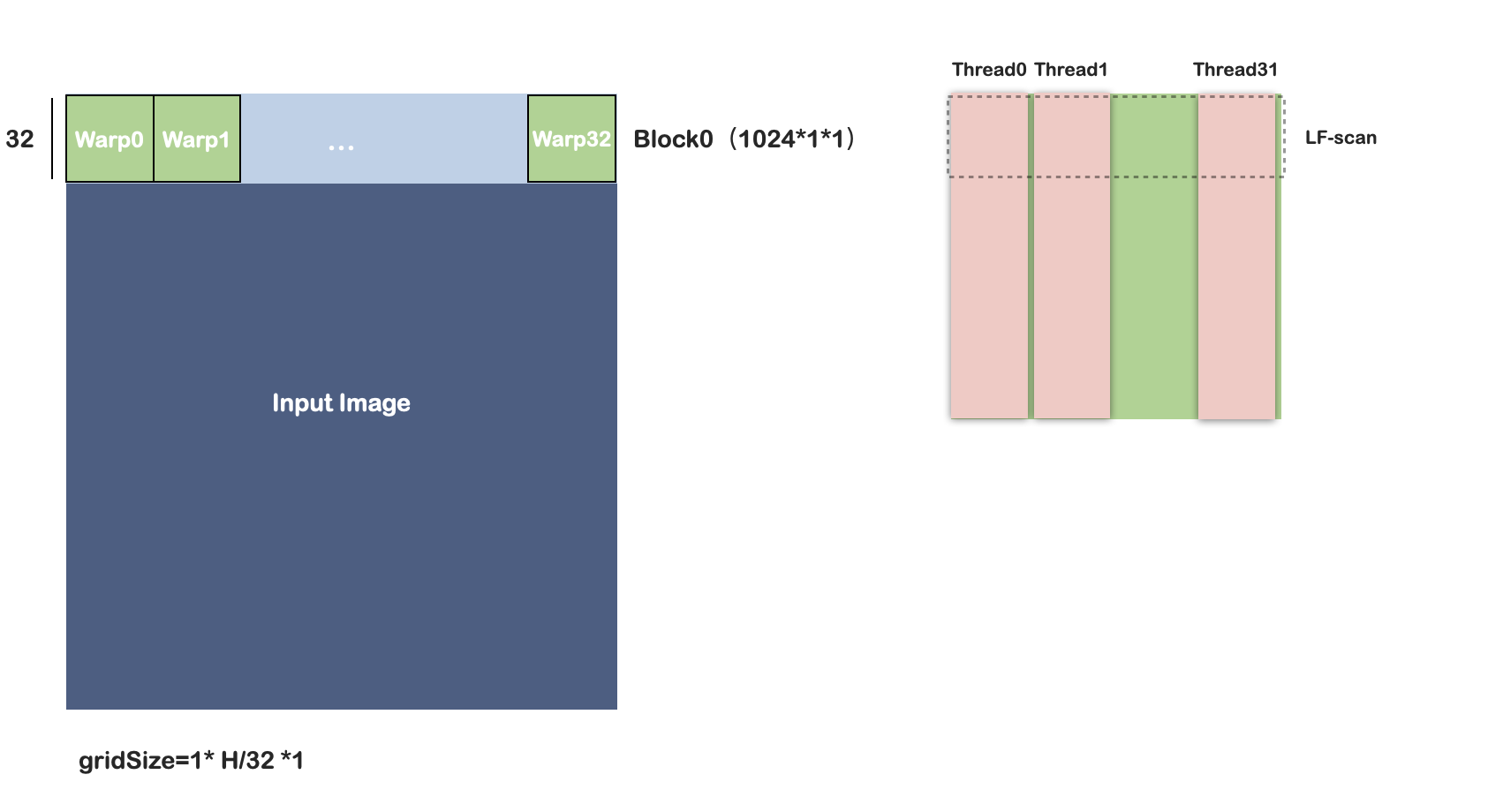
    image.png
    如上图所示，每个block负责32行的数据，每个warp处理32*32的块。
    每个线程读取32个数据，线程之间使用LF-scan（利用shuffle操作）。
    warp之间的通信：
    在一个线程中串行操作，复杂度O(n^2)：
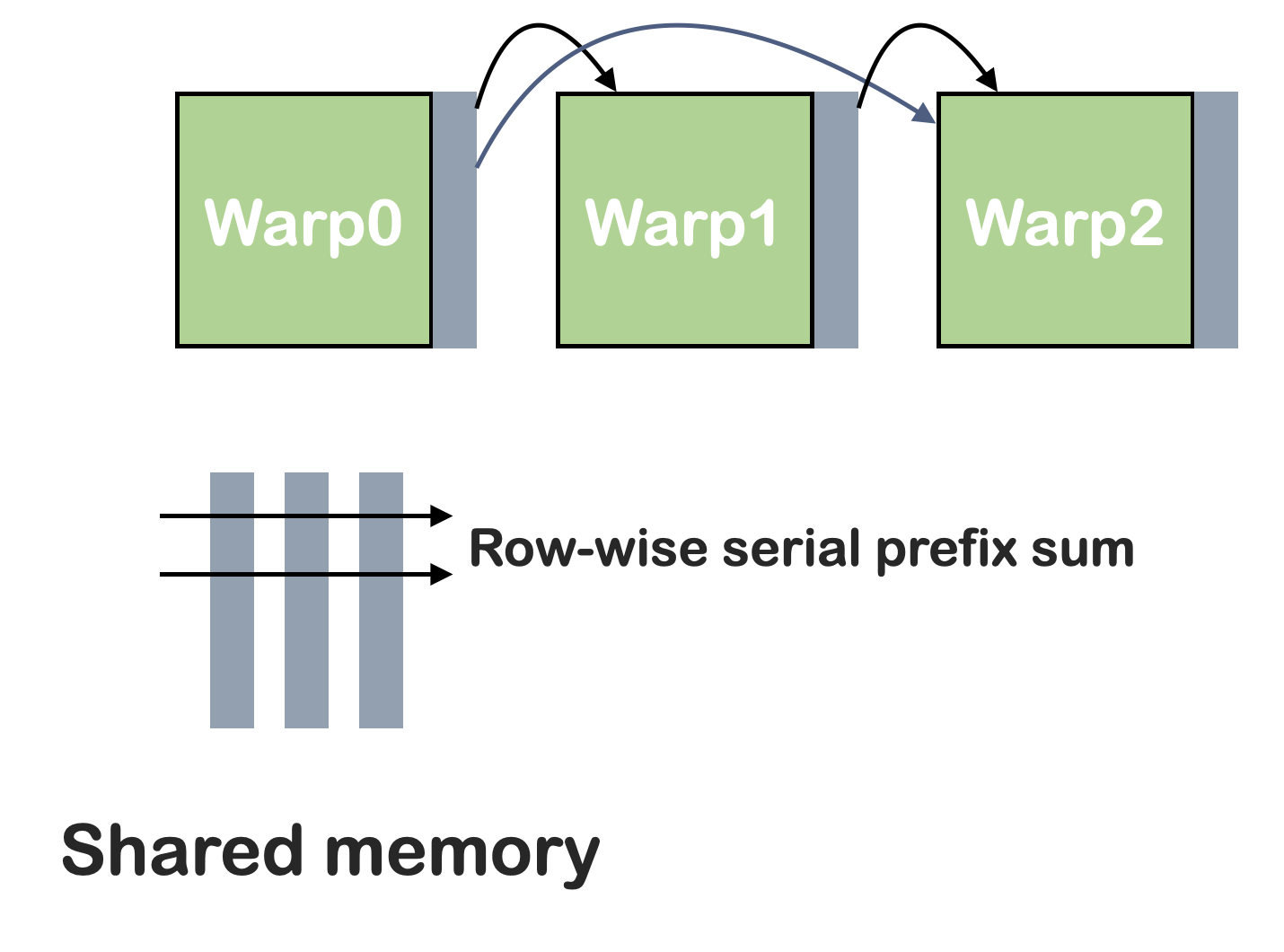
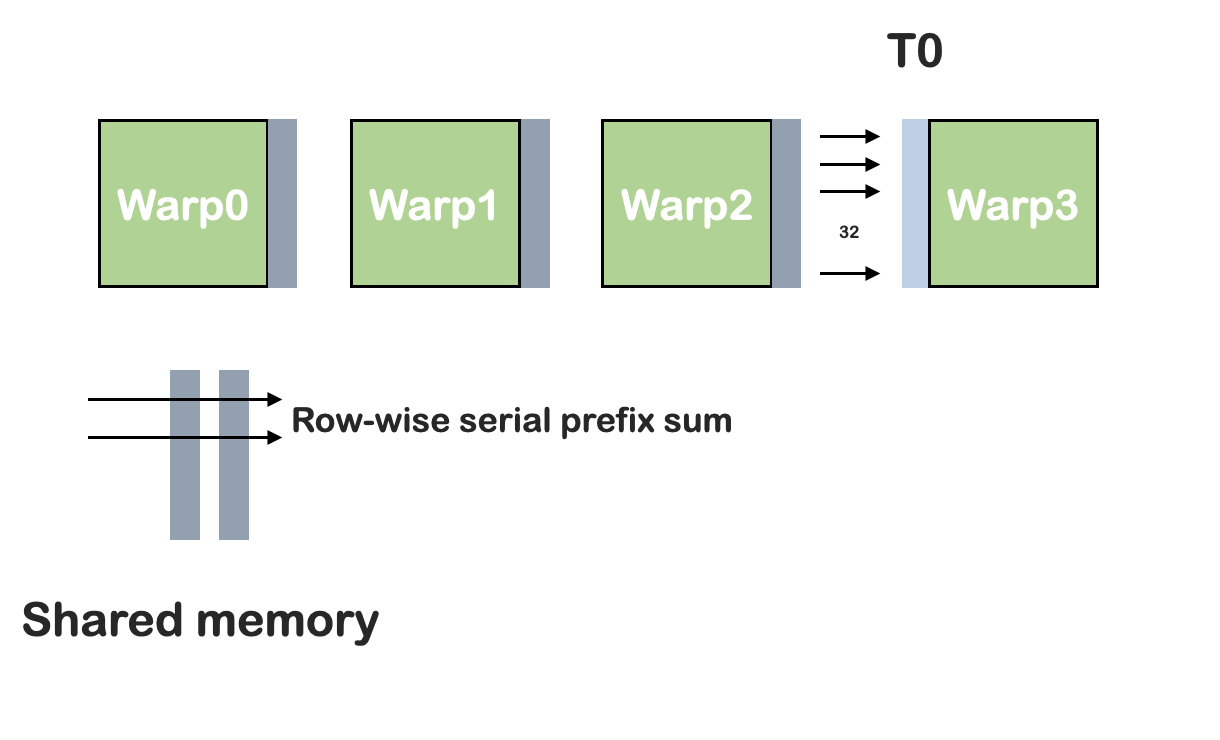
    image.png
    image.png

思考

  1. warp是被调度的基本单元，但并不意味着不同warp之间有先后顺序，也不意味着warp被完整调度。
  2. 为什么转置以后再写回主存，直接rigister-shared memory-rigister的模式完成两次算法IO更少。
  3. 如何处理更大的图像。

方法二：BRLT-ScanRow

与方法1类似，但是先转置再执行scan操作。重复两次。但是论文指出，该方法使用串行扫描算法，并且这种方法效率更高。
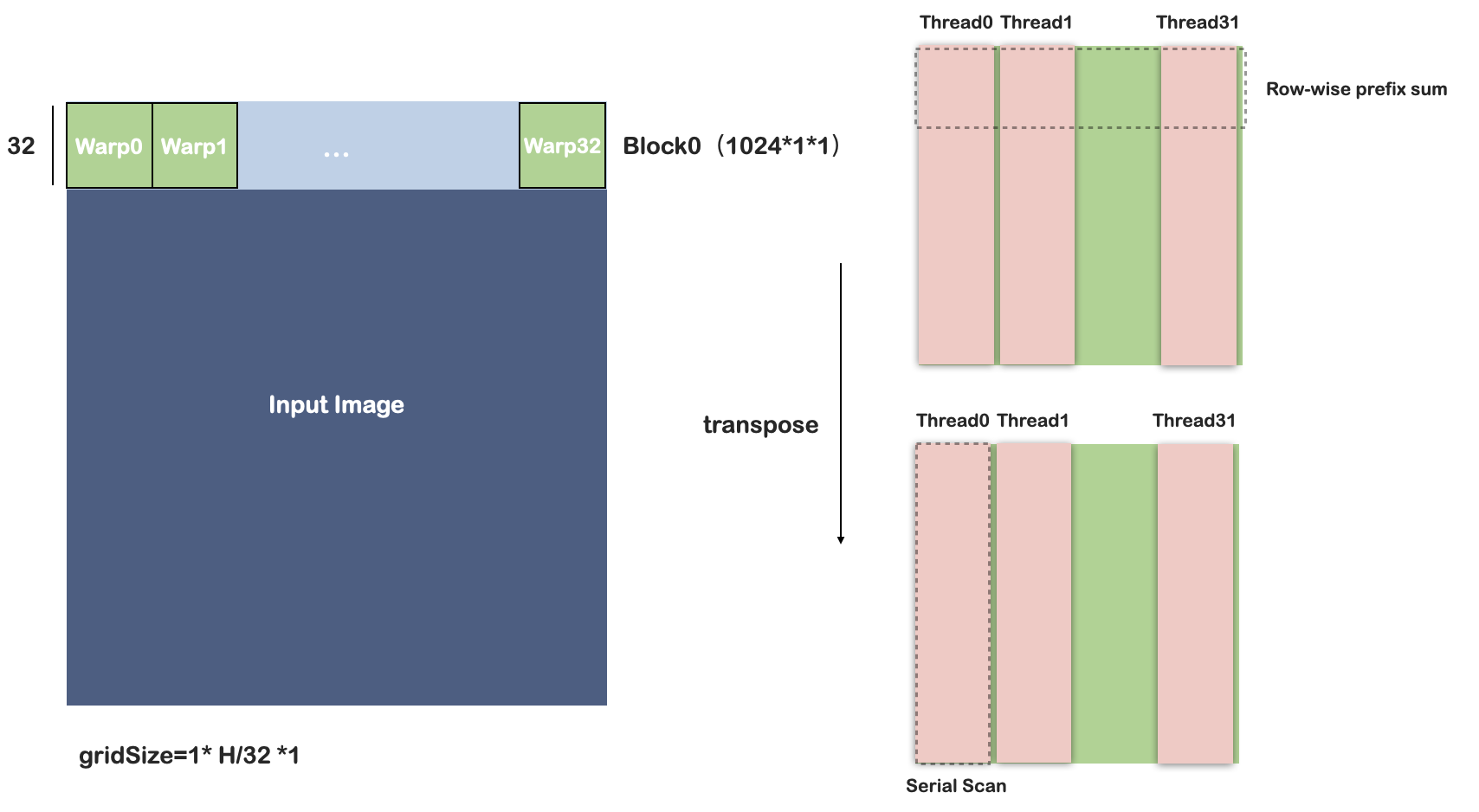
image.png
warp之间使用共享内存通信，但是该方法的每个线程只需要一个位置的preSum，复杂度降低为O(n)
Uploading file...e22h5

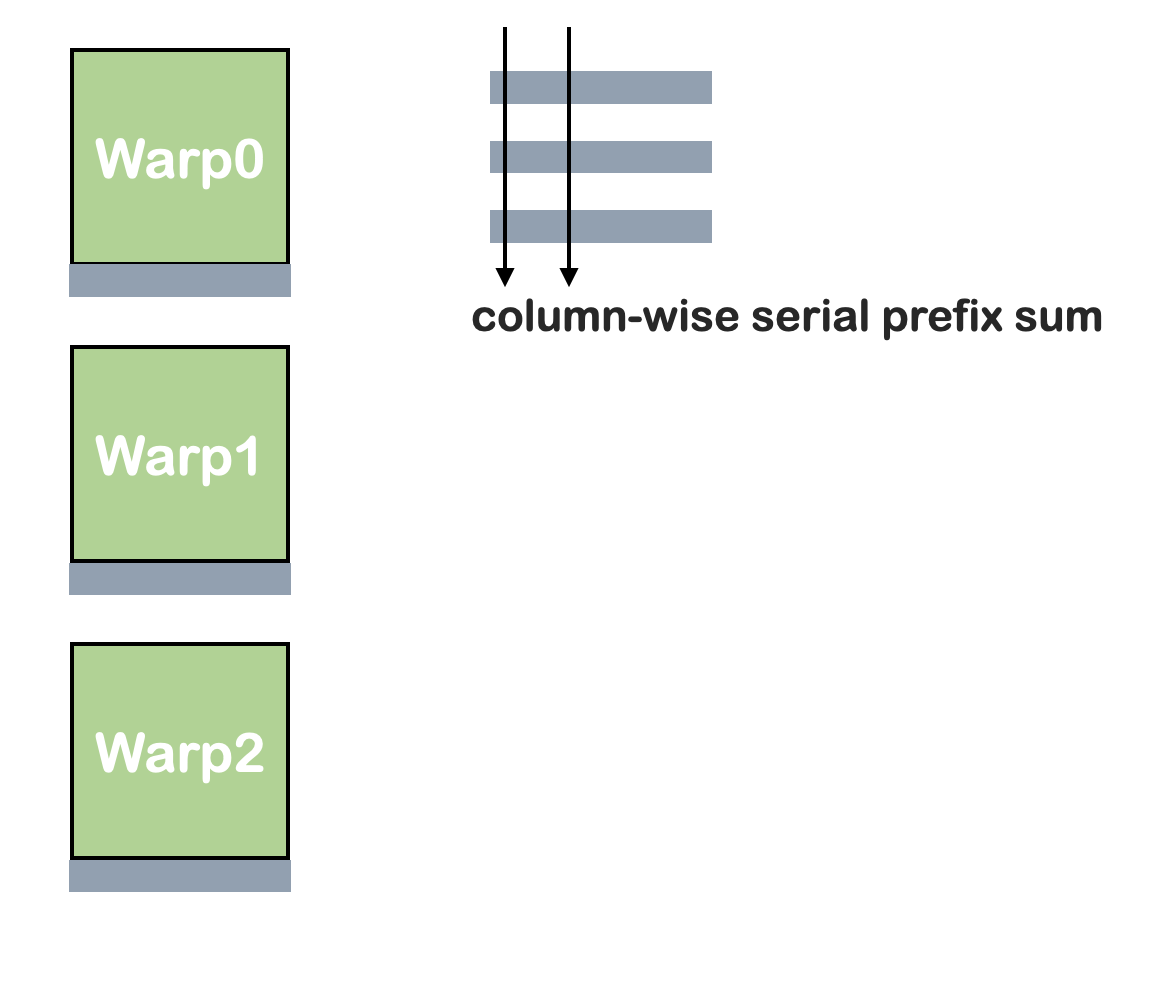
image.png

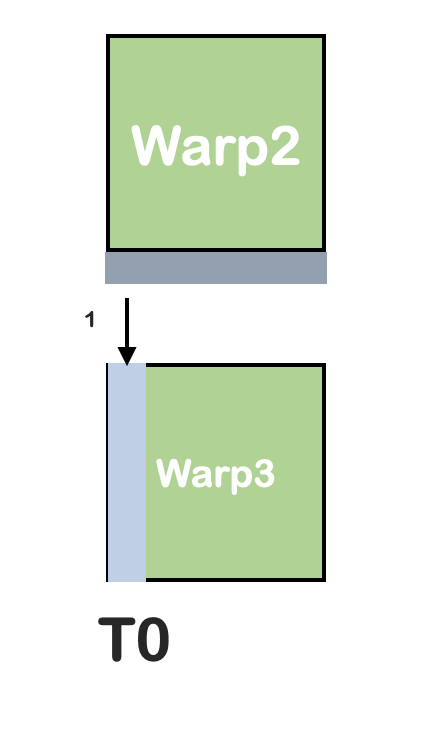
方法三：Register-based ScanRowColumn Method

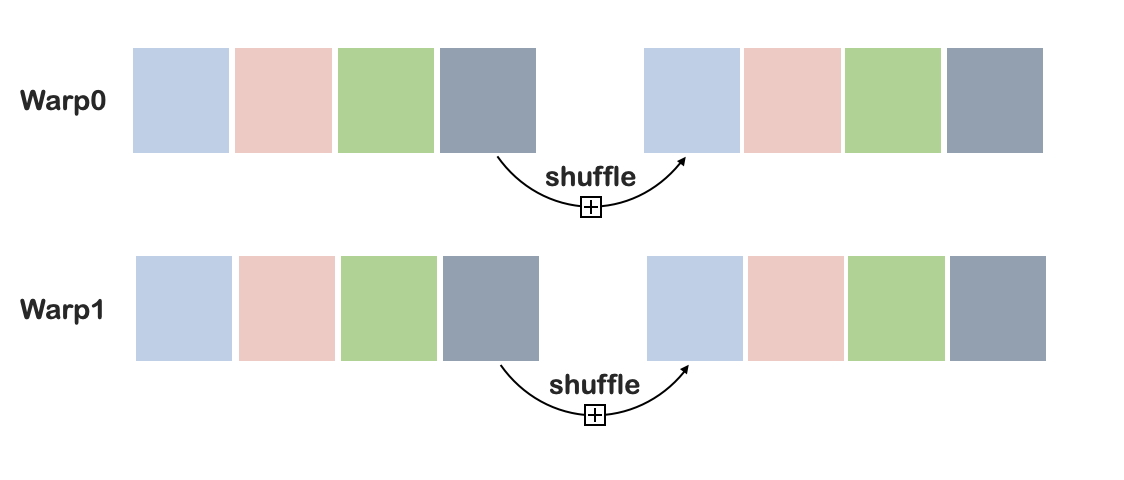
image.png
每个block处理32行的数据，每个warp处理一行的数据。
例如warp0，扫描0-31号元素，使用shuffle操作传递到warp0的第二次扫描的第一个线程上。